Álgebra de funciones derivables I
En este apartado podrás encontrar una conclusión sobre la derivabilidad, algunos ejemplos de funciones derivables y los teoremas sobre álgebra de funciones derivables.

¿Qué debe ocurrir para que una función sea derivable en un punto a?
1) En primer lugar ya sabemos que debe ser continua en a.
2) Pero además, que exista el límite del cociente de Newton y en consecuencia, que se pueda trazar la recta tangente a su gráfica en el punto (a,f(a)).

Los ejemplos vistos en el apartado 1, de este tema así lo confirman. Son funciones que tienen un "quiebre" en a, o la pendiente de la recta tangente no es finita o la gráfica parece muy intrincada en las cercanías de a.

¿Cómo es una función derivable?

Definición
Una función es derivable, si es derivable en todos los puntos de su dominio.

Así, una función derivable, en primer lugar debe ser continua en todos los puntos de su dominio y tener una gráfica "suave", de tal manera que en todos sus puntos sea posible trazar una recta tangente.

Teorema 1 (La derivada de una función constante es cero)

Demostración: Q.E.D.

Teorema 2 (La derivada de la función idéntica es 1)

Demostración: Q.E.D.

Teorema 3 (Derivabilidad de la suma)


Teorema 4 (Derivabilidad del producto)


Teorema 5 (Derivada de una constante por una función)


Teorema 6 (Derivada de la idéntica a la potencia n)

Derivadas de orden superior
Si f es una función derivable, entonces su derivada f ' es a su vez una función, que puede o no ser derivable. Si lo es, entonces, se produce otra función, la derivada de la derivada de f y así sucesivamente. Por ello, es posible definir de manera recursiva las derivadas de orden superior:



Las derivadas de las funciones polinomiales
Con los teoremas vistos en este apartado y con la definición recursiva de las derivadas se tiene una primera conclusión sobre las derivadas de un polinomio:

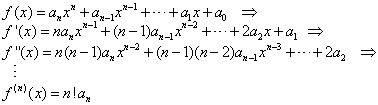
Es decir, las funciones polinomiales son derivables y sus derivadas también y así sucesivamente. Como la derivada enésima es constante, de ahí las demás son cero. Como veremos más adelante, hay funciones cuya derivada no siempre es derivable.

Interpretación de las derivadas de orden superior

Geométrica
y así, se puede extender.

Física
se interpreta como el cambio instantáneo de la velocidad instantánea de una partícula en el tiempo a, es decir, la aceleración de la misma. Y así puede extenderse.

En general
La segunda derivada f ''(a) significa la razón de cambio de f ' respecto a su variable, en a. Y así puede extenderse.