Teoremas importantes I
En este apartado veremos un conjunto de teoremas de mucha importancia para el significado de la derivada.

Teorema 3 (Teorema de Rolle)

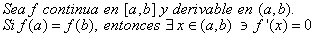
Lo que asegura este teorema es que f alcanza un máximo o mínimo local en (a,b). Al partir de (a,f(a)), si "sube" o "baja", tiene que regresar a (b,f(b)) sin rupturas ni saltos y al ser derivable en (a,b), así debe alcanzar un máximo o un mínimo y como es derivable en (a,b) se tiene que debe ser una función "suave", sin quiebres y entonces la derivada existe y deberá ser cero.

Teorema 4 (Teorema del valor medio)

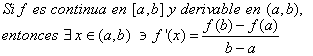
Este teorema es una generalización del Teorema de Rolle. Si f(a) = f(b), tendríamos como caso particular a dicho teorema. El teorema del valor medio asegura que existe x en (a,b), donde la pendiente de la recta tangente es igual a la pendiente de la recta secante que pasa por (a,f(a) y (b,f(b)).

Del teorema 4 (Teorema del valor medio) se desprenden varios corolarios interesantes que ayudan a ir configurando cada vez más, el significado de la derivada.

Corolario 1

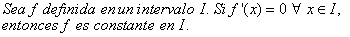
Corolario 2


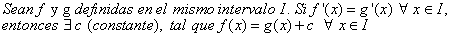
Corolario 3

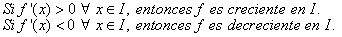
Este corolario 3, permite calcular los intervalos de crecimiento y decrecimiento de una función y combinado con los máximos y mínimos locales facilitan ir configurando la gráfica de una función.

Un problema importante es el trazo de la gráfica de una función y en ese caso es recomendable, determinar:

1. Los puntos críticos de f
2. El valor de f en los puntos críticos
3. El signo de f ' en las regiones entre los puntos críticos
4. Los números x, tales que f(x) = 0, si fuera posible.
5. El comportamiento de f cuando x tiende a más o menos infinito (si fuese posible).

Lo anterior, aunado a una inspección rápida para ver si la función es par o impar, monótona, etc., ayudará mucho a configurar su gráfica. Existe un criterio para los máximos y mínimos locales que sólo depende del comportamiento de f en el punto crítico, como veremos en el siguiente teorema.

Teorema 5

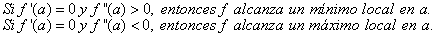
Este teorema 5 es muy útil sobre todo para funciones polinómicas, sin embargo, para muchas funciones la expresión de la segunda derivada es tan complicada, que es preferible recurrir al recomendable punto 3, es decir, a analizar el signo de la primera derivada antes y después de un punto crítico.

Aun más, es posible que f''(a) = 0 y en ese caso, el teorema 5 no proporciona información, puede ser máximo o mínimo local o ninguno de los dos. Esto lo confirma el siguiente teorema.

Teorema 6

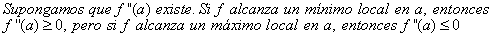
Para confirmar el teorema 5, en estos ejemplos, podrías
calcular el valor de la segunda derivada en cada punto crítico.