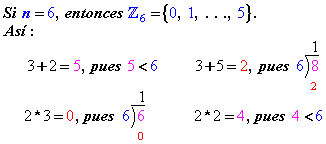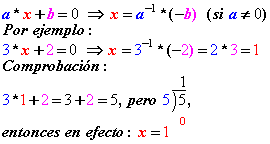Los
enteros módulo n
Existen
otras estructuras algebraicas finitas, que dependiendo del valor de n natural,
son o no, un campo. En el caso de aquellas que no son un campo, se dan
situaciones muy interesantes, como ecuaciones sin solución o leyes
algebraicas que no se cumplen.
El ejemplo más sencillo
Presentamos a continuación la más sencilla de estas estructuras: 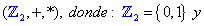
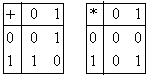
Es relativamente sencillo hacer ver que cumple todos los axiomas de campo.
Similarmente, tenemos: 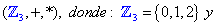
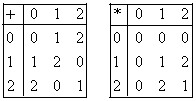
De seguro, las más laboriosas de comprobar sean la asociatividad y la distributiva, pero al igual que la anterior, es posible ver que cumple todos los axiomas de campo.
En general estas estructuras se describen de la siguiente
forma:
Definición

Por
ejemplo
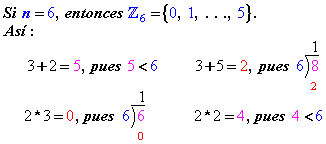
Los
enteros módulo 4 en forma interactiva
Dando
clic en Enteros
Módulo 4, verás la ilustración
interactiva de sus tablas se adición y multiplicación y podrás
observar algunas de sus propiedades, en particular que no conforman un
campo, puesto que falla la existencia del inverso multiplicativo y por
lo mismo no se cumple la respectiva ley de cancelación.
Los
enteros módulo 5 en forma interactiva
Dando
clic en Enteros
Módulo 5, verás la ilustración
interactiva de sus tablas se adición y multiplicación y podrás
observar algunas de sus propiedades, en particular que sí conforman
un campo.
Se
observa fácilmente que las operaciones son cerradas, conmutativas
y que existen neutros e inversos. Es un poco laborioso ver que en efecto
se cumplen las asociativas y la distributiva.
De
lo anterior se desprende que al ser un campo, cumplen todos los teoremas
que demostramos para los reales, en particular las leyes de cancelación
para ambas operaciones.
Así,
en los enteros módulo 5, toda ecuación de la forma:
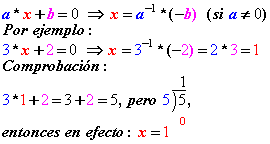
De
manera general
Aunque
aquí no haremos la demostración, se sabe que: 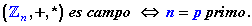
Conclusiones
En
todos los campos se cumplen las leyes de cancelación, tanto para
la adición como para la multiplicación.
En
todos los campos tiene solución cualquier ecuación de la
forma: a*x + b =0
![]()

![]()