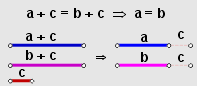
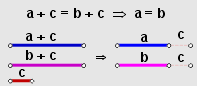
Idea
y Método de la Demostración
La
idea es partir de a,
y mediante una cadena de igualdades llegar a b,
utilizando el llamado Método
Directo.
Para
construir
Para
construir tal cadena de igualdades se deben utilizar exclusivamente los
axiomas
de los reales, las hipótesis
del teorema y desde luego propiedades conocidas de la igualdad, en este
caso la transitividad: Si x
= w y w
= z, entonces
x
= z y el siguiente Principio: "Si en una expresión se sustituye un objeto por otro igual, la expresión resultante es la igual a la anterior". En adelante nos referiremos a éste como Principio de sustitución.
Por ejemplo
![]()
Basta que en la expresión a + c, se sustituya a por b y entonces queda que a + c = b + c.
El
Resultado General
Así,
juntando la ley de cancelación para la adición y el recíproco, mostrado en el ejemplo anterior,
se tiene un resultado más general, es decir:
![]()
Conclusión
Este
resultado permite tanto sumar como cancelar una misma cantidad en ambos
lados de una igualdad, lo cual es de suma importancia en la resolución
de ecuaciones.