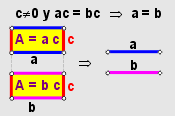
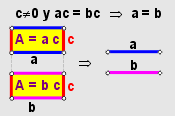
Idea
y Método de la Demostración
La
idea es partir de a,
y mediante una cadena de igualdades llegar a b,
utilizando el llamado Método
Directo.
Para
construir
Para
construir tal cadena de igualdades se deben utilizar exclusivamente los
axiomas
de los reales, las hipótesis
del teorema, teoremas o resultados anteriores y, desde luego propiedades
conocidas de la igualdad, en este caso la transitividad: Si x
= w y w
= z, entonces
x
= z y el Principio de sustitución.
Por ejemplo
![]()
El
Resultado General
Así,
juntando la ley de cancelación para la multiplicación y su recíproco mostrado en el ejemplo anterior,
se tiene un resultado más general, es decir:
![]()
Conclusión
Este
resultado permite tanto multiplicar como cancelar una misma cantidad (distinta
de cero), en ambos lados de una igualdad, lo cual es de suma importancia
en la resolución de ecuaciones.