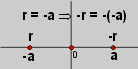
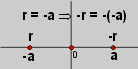
Idea y Método de la Demostración
La idea es hacer ver que -(-a) es inverso aditivo de (-a),  y dado que por el teorema 4, sólo existe un inverso aditivo, entonces a = -(-a).

Así, la idea es iniciar en -(-a) + (-a)  y, mediante una cadena de igualdades llegar a 0, utilizando el llamado Método Directo.

Para construir
Para construir tal cadena de igualdades se deben utilizar exclusivamente los axiomas de los reales, las hipótesis del teorema, teoremas o resultados anteriores y, desde luego, propiedades conocidas de la igualdad, en este caso la transitividad: Si x = w y w = z, entonces x = z y el Principio de sustitución.

En particular se hace uso del Teorema 4 que establece:

Conclusión
Este teorema prepara la demostración de la ley de los signos que dice: el inverso aditivo de a, por el inverso aditivo de b, es ab.